- The Resonance Condition

The Resonance Condition

Consider an isolated nucleus in a steady magnetic field Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{_0}} . The magnetic field breaks the symmetry of free space and defines a particular spatial direction. Suppose that the nucleus possesses an intrinsic "spin" with spin number $I>0$ so that it has an intrinsic magnetic moment (moving/spinning electric charge creates a magnetic field). How does this intrinsic "spin" relate to angular momentum? It is necessary to find this relation explicitly.

We know from quantum mechanics that (on small enough scales) energy appears in discrete bits ( $\hbar$ shows its face ). It is then reasonable to suppose that "spin" energies are also discrete (or quantized). Physical experiments bear out this supposition.

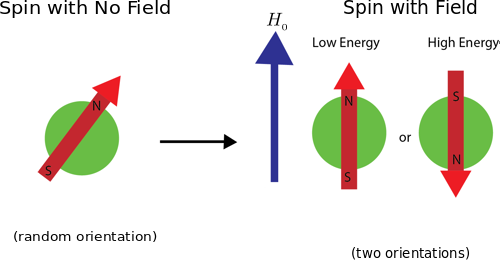
The nucleus will have different energy states depending on the magnitude and direction of the nucleon's magnetic moment. See the figure below for the allowed spin states of a spin-1/2 particle.

The energy of a magnetic dipole moment $\mu$ in a magnetic field $H_{_{0}}$ is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E=-\mu\cdot H_{0}} . If the energy in the system is low enough, most, if not all, of the spins will be parallel to the field (lowest energy state). However, if there is enough energy around then some nucleon's will absorb a bit of energy and will become aligned anti-parallel to the magnetic field.

A careful study of quantum mechanics reveals that the length of the nuclear angular momentum vector is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [I(I+1)]^{1/2}\hbar} but that the only measurable components of this vector are given by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m\hbar} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m} , the magnetic quantum number, may take any of the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (2I+1)} values in the series Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I, I-1, I-2, ... , -(I-1), -I} .

Correspondingly, the nuclear magnetic moment also has Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (2I+1)} components in proportion. We can define Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} as the maximum measurable (observable) component of the magnetic moment.