Permittivity and Permeability of Materials Obstacle Course: Difference between revisions
Jump to navigation
Jump to search
| Line 47: | Line 47: | ||
<br><br><br><br><br><br><br><br><br><br> | <br><br><br><br><br><br><br><br><br><br> | ||
=== * Permittivity of a ''Lossy'' Material From a Capacitance Measurement === | === * Permittivity of a ''Lossy'' Material From a Capacitance Measurement (up to 50 MHz)=== | ||
[[File:RCVdivider.png|right|350px]] | |||
# Employ the guarded-electrode setup above and measure the lossy material's capacitance and conductance. <math>C=\epsilon^'\frac{A}{d}</math> and <math>G=\omega \epsilon^{''} \frac{A}{d}</math>, where <math>\epsilon^'\text{/}</math><math>\epsilon^{''}</math> are, respectively, the real and imaginary parts of the complex permittivity. | # Employ the guarded-electrode setup above and measure the lossy material's capacitance and conductance. <math>C=\epsilon^'\frac{A}{d}</math> and <math>G=\omega \epsilon^{''} \frac{A}{d}</math>, where <math>\epsilon^'\text{/}</math><math>\epsilon^{''}</math> are, respectively, the real and imaginary parts of the complex permittivity. | ||
## Simultaneously measure the voltage across the resistor <math>V_R</math> and Lock-in voltage <math>V_{Lock-in}</math> at <math>V_{out}</math>. Employ a lock-in time constant that is much longer than the period of the AC driving voltage. The lock-in voltage <math>V_{Lock-in}</math> is given by <math>V_{Lock-in}=\frac{1}{2}V_{out} \,\, cos(\theta)</math> , where <math>V_{out}</math> is the voltage across the capacitor and <math>\theta</math> is the phase difference between the AC driving voltage and <math>V_{out}</math> | |||
## The current through the capacitor is given by <math>I_C=V_R/R</math>. The voltage across the capacitor is given by <math>V_{out}=Z_C I_C</math>, where <math>Z_C</math> is the capacitor's impedance. Solve for the impedance <math>Z_C</math>. | |||
## The capacitor's [https://en.wikipedia.org/wiki/Admittance admittance] <math>Y_C</math> is given by <math>Y_C=\frac{1}{Z_C}</math>, where the <math>Re(Y_C)=G</math> (the conductance) and the <math>Im(Y_C)=B</math> (the susceptance). Calculate <math>G</math>. | |||
## Read section 13.1 (pages 106-107) in this [[http://hank.uoregon.edu/wiki/images/b/b5/Measuring_the_Permittivity_and_Permeability_of_Lossy_Materials_-_Solids%2C_Liquids%2C_Metals%2C_Building_Materials_and_Negative-Index_Materials_.pdf paper]]. | |||
## Calculate the relative permittivity <math>\epsilon_r</math> as <math>\epsilon'_r=\frac{C}{C_{air}}</math> and <math>\epsilon''_r=\frac{G}{\omega C_{air}}</math>. | |||
## Do the above procedure for at least three frequencies between 10 MHz and 50 MHz. | |||
## Plot <math>\epsilon'_r</math> and <math>\epsilon''_r</math> as a function of frequency. | |||
Revision as of 18:45, 21 May 2018
PAGE UNDER CONSTRUCTION
Permanent Materials
- 6061 3/8" Al rod stock
- Teflon
- Glass microscope slide
- HP Signal Generator (DC-1 GHz)
- Oscilloscope (at least 1GHz bandwidth)
- Miscellaneous electrical components
Materials to Borrow When Necessary
- Milling machine
- Lathe
Activities
Reading
- Read the Wikipedia articles on permittivity and permeability. With the help of the instructor or TA try to achieve a physical understanding of just what the permittivity and permeability mean in a bulk material.
- Read the first three sections of this paper (pages 1-27). Pay particular attention to the permittivity () / capacitance and permeability () / inductance associations.
Capacitance Techniques (Below 10MHz)
* Permittivity of a Lossless Material From a Capacitance Measurement
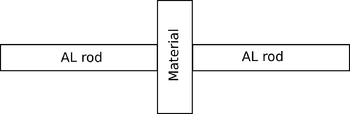
- Place three samples (air, Teflon, glass) between the aligned and polished ends of two 3/8" diameter, 1/2" lengths of 6061 Al rods (as shown at right). should be on the order of 1 mm. Measure the capacitances and, from the known surface area and spacing , determine the material's relative permittivity. (for a capacitor with no fringing fields).
- How do your measured permittivity values compare to standard reference values?
- Use this web applet to build a capacitor and observe the field lines . Are there fringing fields?
(air): 1.000536
(Teflon): 2.1
(glass): 3.7-10
* A Better Permittivity-Capacitance Measurement of a Lossless Material
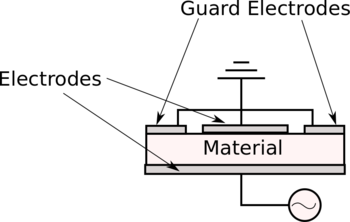
- Use this web applet to build a guarded-electrode capacitor (as shown at the right) and observe the field lines . Are there fringing fields?
- Measure the three permittivities (air, Teflon, glass) again using this guarded-electrode setup.
- How do these results compare to your first (unguarded) measurements?
- How do these results compare to the standard values?
The measurements above for a lossless material amount to requiring the permittivity to be real (as opposed to complex). However, for a lossy material, the permittivity is complex and we need an additional characteristic (beyond simply the capacitance) to characterize the material. This additional characteristic is the conductance . The measurement below will include the conductance of the material.
* Permittivity of a Lossy Material From a Capacitance Measurement (up to 50 MHz)
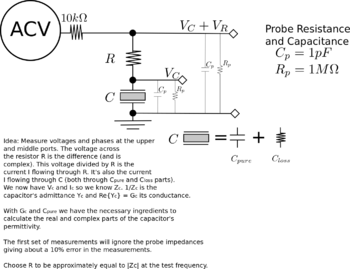
- Employ the guarded-electrode setup above and measure the lossy material's capacitance and conductance. and , where are, respectively, the real and imaginary parts of the complex permittivity.
- Simultaneously measure the voltage across the resistor and Lock-in voltage at . Employ a lock-in time constant that is much longer than the period of the AC driving voltage. The lock-in voltage is given by , where is the voltage across the capacitor and is the phase difference between the AC driving voltage and
- The current through the capacitor is given by . The voltage across the capacitor is given by , where is the capacitor's impedance. Solve for the impedance .
- The capacitor's admittance is given by , where the (the conductance) and the (the susceptance). Calculate .
- Read section 13.1 (pages 106-107) in this [paper].
- Calculate the relative permittivity as and .
- Do the above procedure for at least three frequencies between 10 MHz and 50 MHz.
- Plot and as a function of frequency.


























