- The Resonance Condition: Difference between revisions
| Line 19: | Line 19: | ||
---- | ---- | ||
This separation is often written as <math>g \mu_{_0} H_{_0}</math>, where <math>g=\frac{\mu}{\mu_{_0}I}</math> is called the ''splitting factor'' | This separation is often written as <math>g \mu_{_0} H_{_0}</math>, where <math>g=\frac{\mu}{\mu_{_0}I}</math> is called the ''splitting factor'' or the ''g-factor''. The selection rules (derived from energy and momentum conservation arguments), state that <math>m</math> can change by <math>\pm 1</math>. Transitions that involve a change of <math>m</math> by <math>\pm 1</math> require (or produce) circularly polarized light (for momentum conservation). | ||
'''A quantum of energy <math>\lambda</math> can therefore excite transitions between levels if it has the same energy as the level spacing and is circularly polarized. That is, if <math>h\nu_{_0}=g\mu_{_0}H_{_0}</math>, where <math>\nu_{_0}</math> is the frequency of the electromagnetic radiation supplying the quanta of energy and its magnetic field is circularly polarized in the plane perpendicular to the steady magnetic field .''' | '''A quantum of energy <math>\lambda</math> can therefore excite transitions between levels if it has the same energy as the level spacing and is circularly polarized. That is, if <math>h\nu_{_0}=g\mu_{_0}H_{_0}</math>, where <math>\nu_{_0}</math> is the frequency of the electromagnetic radiation supplying the quanta of energy and its magnetic field is circularly polarized in the plane perpendicular to the steady magnetic field .''' | ||
Revision as of 01:54, 8 February 2019
The Resonance Condition
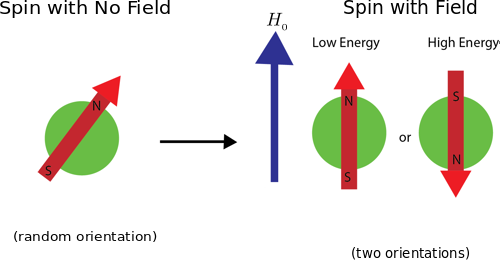
Consider an isolated nucleus in a steady magnetic field . The magnetic field breaks the symmetry of free space and defines a particular spatial direction. Suppose that the nucleus possesses an intrinsic "spin" with spin number so that it has an intrinsic magnetic moment (moving/spinning electric charge creates a magnetic field). How does this intrinsic "spin" relate to angular momentum? It is necessary to find this relation explicitly.
We know from quantum mechanics that (on small enough scales) energy appears in discrete bits ( shows its face ). It is then reasonable to suppose that "spin" energies are also discrete (or quantized). Physical experiments bear out this supposition.
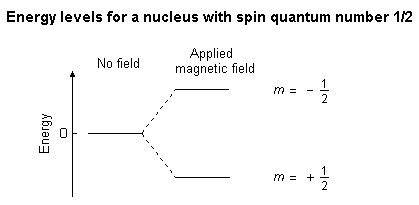
The nucleus will have different energy states depending on the magnitude and direction of the nucleon's magnetic moment. See the figure below for the allowed spin states of a spin-1/2 particle.
The energy of a magnetic moment in a magnetic field is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E=-\mu\cdot H_{0}}
. If the energy in the system is low enough, most, if not all, of the spins will be parallel to the field (lowest energy state). However, if there is enough energy around then some nucleons will absorb a bit of energy and will become aligned anti-parallel to the magnetic field.
A careful study of quantum mechanics reveals that the length of the nuclear angular momentum vector is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [I(I+1)]^{1/2}\hbar} but that the only measurable components of this vector are given by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m\hbar} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m} , the magnetic quantum number, may take any of the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (2I+1)} values in the series Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I, I-1, I-2, ... , -(I-1), -I} .
Correspondingly, the nuclear magnetic moment also has Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (2I+1)} components in proportion. This is a consequence of "space quantization" demonstrated so famously by Stern and Gerlach in 1922.
We can define Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} as the maximum measurable (observable) component of the magnetic moment. Even though the length of the magnetic moment vector is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [(I+1)/I]^{1/2}\mu } , the quantity of physical interest is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} and for this reason workers in the field usually refer to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} as the magnetic moment. As mentioned above, the energy levels of the nuclear magnet in the field Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{_0}} are given by the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (2I+1)} values of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -m\mu H_{_0}/I} . In the general case, this results in a set of equally-spaced levels with separation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu H_{_0}/I} between adjacent levels.
This separation is often written as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g \mu_{_0} H_{_0}} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g=\frac{\mu}{\mu_{_0}I}} is called the splitting factor or the g-factor. The selection rules (derived from energy and momentum conservation arguments), state that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m} can change by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pm 1} . Transitions that involve a change of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m} by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pm 1} require (or produce) circularly polarized light (for momentum conservation).
A quantum of energy Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda} can therefore excite transitions between levels if it has the same energy as the level spacing and is circularly polarized. That is, if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h\nu_{_0}=g\mu_{_0}H_{_0}} , where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nu_{_0}} is the frequency of the electromagnetic radiation supplying the quanta of energy and its magnetic field is circularly polarized in the plane perpendicular to the steady magnetic field .
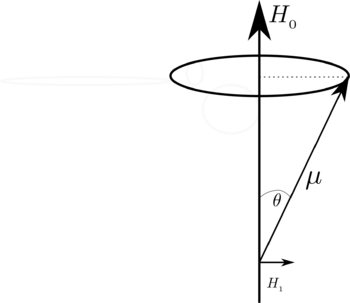
For a proton the value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g} is ~ 5.58. Therefore, in a field of 5000 Gauss, the resonance frequency is ~ 21.3MHz. This satisfies energy conservation requirements. To understand the polarization requirements consider the figure below.
Consider a magnetic dipole Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} placed in a magnetic field Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{_0}} as shown above. The dipole precesses about the direction of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{_0}} . The rate of precession is given by the well-known Larmor frequency Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_{_0}=\gamma H_{_0}} . Now suppose that an additional small magnetic field Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{_1}} is applied at right angles to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{_0}} This "transverse" field will tend to cause Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} to increase its angle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} (increasing the dipole's energy). If the small field Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{_1}} is made to rotate around the axis defined by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{_0}} at the same frequency as that at which the dipole Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} precesses (the Larmor frequency) then the field Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H_{_1}} will cause the angle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} to steadily increase (adding energy to the nucleon).
A resonance therefore occurs when the angular frequency of the transverse field is equal to the dipole's Larmor precession frequency. Although a rotating transverse magnetic field is quite practicable, it is usually much simpler to provide a linearly oscillating field. That is because a linearly oscillating field may be regarded as the superposition of two rotating fields. Resonance occurs when one of these two rotating fields has the correct rotation direction (with respect to the precessing dipole). It is generally not possible to tell which rotating field component (CW or CCW) is utilized. This information is only required when it is desired to find the sign of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu} , which determines the direction of Larmor precession.