- The Resonance Condition: Difference between revisions
Jump to navigation
Jump to search
Created page with "===The Resonance Condition=== Consider an isolated nucleus in a steady magnetic field <math>H_{_0}</math>. The magnetic field breaks the symmetry of free space and defines a..." |
No edit summary |
||
| Line 1: | Line 1: | ||
===The Resonance Condition=== | ===The Resonance Condition=== | ||
Consider an isolated nucleus in a steady magnetic field <math>H_{_0}</math>. The magnetic field breaks the symmetry of free space and defines a particular spatial direction. Suppose that the nucleus possesses an intrinsic "spin" with spin number <math>I>0</math> so that it has a magnetic moment. | Consider an isolated nucleus in a steady magnetic field <math>H_{_0}</math>. The magnetic field breaks the symmetry of free space and defines a particular spatial direction. Suppose that the nucleus possesses an intrinsic "spin" with spin number <math>I>0</math> so that it has a magnetic moment. We know from quantum mechanics that (on small enough scales) energy appears in discrete bits ( <math>\hbar</math> shows its face ). It is then reasonable to suppose that "spin" energies are also discrete (or quantized). Physical experiments bear out this supposition. | ||
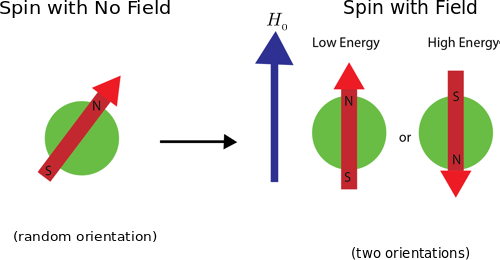
The nucleus will have different energy states depending on the magnitude and direction of the nucleon's magnetic moment (see figure below).<br><br> | |||
We can define <math>\mu</math> as the maximum measurable component of the magnetic moment. | [[File:Magneticfieldapp.png]] | ||
We can define <math>\mu</math> as the maximum measurable (observable) component of the magnetic moment. | |||
Revision as of 19:14, 7 February 2019
The Resonance Condition
Consider an isolated nucleus in a steady magnetic field . The magnetic field breaks the symmetry of free space and defines a particular spatial direction. Suppose that the nucleus possesses an intrinsic "spin" with spin number so that it has a magnetic moment. We know from quantum mechanics that (on small enough scales) energy appears in discrete bits ( shows its face ). It is then reasonable to suppose that "spin" energies are also discrete (or quantized). Physical experiments bear out this supposition.
The nucleus will have different energy states depending on the magnitude and direction of the nucleon's magnetic moment (see figure below).
We can define as the maximum measurable (observable) component of the magnetic moment.