RF Signals: Difference between revisions
Aplstudent (talk | contribs) No edit summary |
No edit summary |
||
| (66 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
RF (short for Radio Frequency) signals are sinusoidal waves with frequencies | RF (short for Radio Frequency) signals are sinusoidal waves with frequencies in the MHz and GHz range. | ||
While there are RF sources designed specifically for these frequencies, our good friend the Rigol Function Generator can produce frequencies in the lower end of the RF spectrum and should be sufficient for investigating RF signals. These were discussed in detail [[Function Generators and Oscilloscopes|here]]. You should review their operation if needed, especially the section on performing Fourier Transforms, as they will be used extensively below. | |||
For this module, you will need | |||
<ul> | |||
<li> Rigol DG1022 Function Generator (or similar)</li> | |||
<li> Rigol DS1102E Oscilloscope (or similar)</li> | |||
<li> Micro-circuits ZAD-1 RF mixer</li> | |||
<li> A selection of BNC cables</li> | |||
<li> A few coaxial-to-BNC adaptors</li> | |||
<li> Thorlabs Variable Resistance Terminator</li> | |||
</ul> | |||
== Measuring RF Power == | |||
Connect the output of channel 1 of the function generator through the terminator (set to 50ohm) to channel 1 of the oscilloscope. | |||
<ol> | |||
<li> Set channel 1 of the function generator to create a 1V amplitude sine wave with a frequency of 4MHz.</li> | |||
<li> Set the horizontal and vertical scales of the scope to view the wave. Make sure the trigger for the scope is set to be on channel 1.</li> | |||
<li> Use the scope's measure function (or the scope's cursor) to get the amplitude of the wave. Is it what you expect? What is the amplitude if you remove the terminator? Does that make sense?</li> | |||
<li> Use the math menu to create a fourier transform of the signal. With the cursor, does the frequency the scope reads match what the setting from the scope? If it doesn't, why do you think that might be?</li> | |||
</ol> | |||
== Termination and Impedance Matching == | |||
We discussed in the function generator and oscilloscope module the importance of impedance matching. To do this, we'll use a circulator (or, rather, a bi-directional coupler as a circulator). A circulator has three ports:, A, B and C. Signals that flow <i>into</i> port A is sent out of port B. Signals that flow into port B is sent out of port C. Signals that flow into port C are sent out of port A. | |||
This is particularly useful for looking at impedance matching. As discussed in the function generator/oscilloscope module, if the impedances, measured in ohm, of two electrical elements signals that change in time can be reflected off one end and back towards the other end. If in between these two elements there is a circulator, the reflected signal will be sent to third port rather than going to the original source of the signal. Measuring the voltage on this third port lets us measure the signal that is reflected from one of the circuit elements. | |||
<ol> | |||
<li> Attach the coupler as follows | |||
<ul> <li>The output of Channel 1 of the signal generator should be attached to the OUTPUT port of the coupler. This is port A of the circulator.</li> | |||
<li> The INPUT port of the coupler should be attached directly to channel 1 of the oscilloscope. This is port B of the circulator.</li> | |||
<li> The COUPLED port of the coupler should be attached, through a 50-ohm terminator, to channel 2 of the oscilloscope. This is port C of the circulator.</li> | |||
<li> In this configuration, the signal from the function generator will flow through port A (output) to port B (input) and then to the oscilloscope's channel 1. Any of that signal that is reflected from channel 1 will flow into port B (input) to port C (coupled) and then to the oscilloscope channel 2.</li> | |||
<li>Yes, it's weird that port A of the circulator is the input port of the coupler, but functioning as a circulator is not really the purpose of the coupler, which is nominally used to combine two signals (from the input and the coupled ports) into an output port. But, it can function as a circulator (or sometimes called a "reflectometer") so we'll use it as one.</li> | |||
</ul></li> | |||
<li> Good job! Now disconnect what you just connected. We're going to use a different setup first. | |||
<ul><li>Connect the output of channel 1 of the function generator directly to channel 1 of the oscilloscope. Set the frequency of the function generator to create a 0.5V amplitude, 5Hz sine wave. </li> | |||
<li>Set the oscilloscope to trigger off channel 1 in edge mode and set the trigger level to something value a little larger than 0V (but less than 0.5V, of course). Make sure the vertical axis of the scope will show the entirety of your wave and the horizontal axis should be at least 100ms/division. | |||
<li> In the trigger menu of the oscilloscope, change the sweep type to single - this will record a single (duh) trace of the oscilloscope when it is triggered and display just that one trace. The screen should erase any plot and the tun/stop button should turn green. If it red, press it and the screen should clear. The scope is now waiting for a trigger.</li> | |||
<li> On the function generator, press the "burst" button. Use the blue buttons under the scope the set the mode to "Ncycle" (the first menu option, don't set it to gated), the number of cycles should be 1, the phase should be 0 and the delay should be 0s. Now press the button under "Trigger" and then the button under "Source". Change the source to "Manual" and stay in this menu. Pressing the button under "manual" again will create a pulse as you defined it above. Try it.</li> | |||
<li> Did that work? Good. Trigger the function generator again. What happened with the oscilloscope? Pressing the red "RUN/STOP" button will clear the screen and allow you to trigger it again. Do this. Cool, huh?</li> | |||
</ul> | |||
</li> | |||
<li> Now change the output of channel 1 to a 4MHz square wave. Change the horizontal scale of the oscilloscope so that it can show your wave (in burst mode, the frequency is really only setting the period of the wave as there isn't really a frequency as the wave won't repeat).</li> | |||
<li> NOW, attach the coupler as discussed above. Trigger the scope. Any signal on channel 2 is the signal that is reflected from the oscilloscope's channel 1 input. Weird, huh?</li> | |||
<li> Put the variable terminator in line with the input to channel 1 of the oscillosope. Repeat the triggering for various termination resistances. | |||
<ul><li>Note how the height of the reflected signal and the height of the measured signal change with the termination resistance, specifically how does the measured signal voltage compare to the output voltage when you terminate with 50-ohm? </li> | |||
<li> Why is a 50-ohm terminator often referred to as a 3dB?</li> | |||
<li> How does the phase of the reflected wave compare to that of the original wave? For this, you may want to have the terimator's resistance high and use a sine wave.</li> | |||
<li>How does this compare to reflections for light off a medium with a higher refractive index? How does it compare to reflections of light off a medium with a lower refractive index?</li> | |||
</ul> | |||
<li> Add another variable terminator to the input to channel 1 (it should have two connected together now). Set both terminators to 50ohm. | |||
<ul> | |||
<li>What is the total input impedance of the oscilloscope now?</li> | |||
<li>How does this compare to the 50ohms impedance of the function generator?</li> | |||
<li> What happened to the phase of the reflected wave? How does it compare to the original wave?</li> | |||
<li> Does this agree with the your comparison to reflected light waves above? Complete the table below.</li> | |||
</ul> | |||
</ol> | |||
<center> | |||
{| class="wikitable" | |||
|- | |||
! | |||
! Light <br> (Refractive Index) | |||
! Electrical Signal <br> (Impedance) | |||
|- | |||
! Reflection off lower <br> index/impedance medium | |||
| | |||
| | |||
|- | |||
! Reflection off higher <br> index/impedance medium | |||
| | |||
| | |||
|} | |||
<b>Change in Phase after Reflection</b> | |||
</center> | |||
== Splitters == | |||
Splitters are fairly straight forward as they just split an RF signal into two outputs. | |||
<ol> | |||
<li>Plug the output of channel 1 of the function generator into the S port of the splitter. Connect the two channels of the oscilloscope to outputs 1 and 2 of the splitter (make sure you match impedance appropriately).</li> | |||
<li> Set the output of channel 1 to 10Mhz and a 1V amplitude.</li> | |||
<li> What is the frequency of each wave on the oscilloscope? Does it agree with your 10MHz input? If it doesn't, why not?</li> | |||
<li> Estimate the amplitudes of the two waves on the oscilloscope. How doe they compare to the input amplitude from the function generator? Why do you think they are related this way?</li> | |||
<li> Estimate any phase difference between the two signals on the oscilloscope. How does that phase difference compare to the phase difference listed in the data sheet for the splitter?</li> | |||
</ol> | |||
You can also use splitters as <i>combiner</i>. | |||
<ol start=6> | |||
<li> Put a 3MHz, 1V amplitude sine wave into port 1 of the splitter.</li> | |||
<li> Put a 7MHz, 1V amplitude sine wave into port 2 of the splitter.</li> | |||
<li> Connect the S port of the splitter to the oscilloscope and and take a fourier transform of the signal. What frequencies are present?</li> | |||
</ol> | |||
== Mixers == | |||
Mixers combine RF frequencies, either taking their sum or their difference. Each mixer has 3 inputs | |||
<ol> | |||
<li> Local Oscillator(LO)</li> | |||
<li> Radio Frequency (RF) </li> | |||
<li> Intermediate Frequency (IF)</li> | |||
</ol> | |||
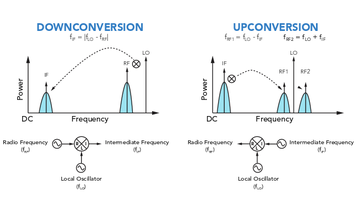
The LO port is <i>always</i> an input. The other two ports change whether they are an input or output depending on your application. For simplicity, we'll assume that the LO signal is always the largest of the two inputs. | |||
If you would like an output that is SMALLER than 2nd (non-LO) input, the RF port is the input and the IF port is the output. Specifically, the output, IF, is the difference between the inputs: | |||
<center><math>f_{IF}=|f_{LO}-f_{RF}|</math></center> | |||
This is called down-conversion, as it takes two signals and creates a third that is <i>lower</i> in frequency than both of them. | |||
If, on the other hand, you want to create a signal that is larger than the inputs, the RF is the output and the IF is in the input: | |||
<center><math>f_{RF2}=f_{LO}+f_{IF}</math></center> | |||
additionally, you will actually get a 2nd frequency that is (again) the difference between the inputs: | |||
<center><math>f_{RF1}=f_{LO}-f_{IF}</math></center> | |||
This is called upconversion because it creates two signals that are <i>larger</i> than the input signal (unless, of course, the IF input is larger than half the LO signal). | |||
The two conversion types are illustrated below. | |||
[[File:mixer-combos.png|x200px|thumb|center|RF Mixer frequency conversion. Image from [http://www.markimicrowave.com/assets/appnotes/mixer_basics_primer.pdf Marki microwave's Mixer Basics Primer].]] | |||
This is how mixers work ideally, but in practice the output signals contain many combinations of the input signals, which can be confusing. We'll see that below. Additionally, because the frequencies are being combined, the waveforms that are produced is very complex and difficult to analyze just from looking at it, so we'll use the FFT function of the oscilloscope to look at the spectrum of the created wave. | |||
We'll look at <b>down-conversion</b> first. | |||
<ol> | |||
<li> Use channel 2 of the function generator as the LO input and set it t0 4MHz and an <i>amplitude</i> of 0.25V.</li> | |||
<li> Use channel 1 of the function generator as the RF input and set the amplitude to 0.25V. Set the frequency to 3MHz.</li> | |||
<li> Connect the IF output of the mixer to channel 1 of the oscilloscope. Set the horizontal scaling to 500ns/division.</li> | |||
<li> How does the signal look? Use the Y-cursor on the oscilloscope to estimate some frequencies you see in the signal (recall that the cursor menu automatically shows you frequency information as <math>|1/\Delta x|</math> where <math>\Delta x</math> is the difference between the locations of cursors A and B).</li> | |||
<li> Now have the function generator perform a fourier transform on the data. Adjust the scales of the math window appropriately. Use the cursors to estimate the frequencies of the peaks shown. Does this agree with what you measured above?</li> | |||
<li> Adjust the frequency of channel 1 and observe how the shape of the wave changes and how the locations of the peaks in the FFT change.</li> | |||
<li> Obviously, this mixer is not perfect. Rather than just getting the difference between the two signals, you get a bunch of other combinations of them of the form <math>f_{out}=\left|n f_{LO}+m f_{RF}\right|</math> where n and m can be any integer (including negative values). | |||
<ul> | |||
<li> For an ideal mixer, what are the values for n and m?</li> | |||
<li> For each peak in the spectrum, what values are the appropriate values for m and n? (hint, you might be helped by looking at how the peaks move if you change the RF frequency a little).</li> | |||
<!-- The students should only get ODD values for m and n and they should probably be combinations of {-3, -1, 1, 3} --> | |||
<li> What do you note about the values of m and n?</li> | |||
</ul> | |||
</li> | |||
</ol> | |||
Now, let's look at <b>up-conversion</b>. | |||
<ol start="8"> | |||
<li> Use channel 2 of the function generator as the LO input and set it t0 4MHz and an <i>amplitude</i> of 0.25V.</li> | |||
<li> Use channel 1 of the function generator as the IF input and set the amplitude to 0.25V. Set the frequency to 3MHz.</li> | |||
<li> Connect the RF output of the mixer to channel 1 of the oscilloscope. Set the horizontal scaling to 500ns/division.</li> | |||
<li> How does the spectrum of the signal compare to the down-conversion spectrum?</li> | |||
<li> What frequencies of the largest few peaks in the spectrum?</li> | |||
</ol> | |||
Using the mixer as you have above is effectively doing a <b>heterodyne</b> measurement on the signal. A heterodyne measurement takes two signals with different frequencies and measures the frequency difference and sum between them. This is a common technique in optics experiments (although often the sum of two frequencies for optical signals is well beyond the limits of a photo-detector). | |||
There is a another technique called a <b>homodyne</b> measurement, which uses the same (hence, <i>homo</i>dyne) signal for both the LO signal and the RF/IF signal after something has been done to the RF signal so we actually get a frequency difference. Let's see why this is useful. | |||
<ol start=13> | |||
<li> Use the mixer as a down converter and look at a 6MHz LO and 3MHz RF signal on channel 1 of the oscilloscope (including looking at the fourier transform</li> | |||
<li> Use a splitter to make a copy of a 3MHz, 1V amplitude signal from channel 1 of the function generator.</li> | |||
<li> Attach one </li> | |||
</ol> | |||
== Attenuation and Filtering == | |||
Attach channel 1 of function generator through one of the 5MHz low-pass filters to the oscilloscope (note that the low-pass filter is 50-ohm terminated, so we don't need to use a terminator). The function generator should produce a 0.25V amplitude sine wave. | |||
<ol> | |||
<li> Set the scope to trigger on channel 1, but set the trigger mode to "slope" - that is the scope will trigger based on what the slope of the signal is. Set the 'When" menu to the top option - a rising slope with a greater than symbol (>). This will trigger the scope whenever it encounters a slope that is larger than a set value. | |||
<ul> | |||
<li> To set this value, use the "time" menu item to look at how the signal changes over some window. Set it to 1 μs, so that the voltage on channel 1 is compared over a range of 1us. </li> | |||
<li> Use the trigger level knob to change the "upper level" of the change you are looking for. The "low level" is set to -4mV. The difference between the two level is the voltage change you are looking for to trigger from. Set the Up Lvl to 0 mV.</li> | |||
<li> So, the trigger slope is the difference between the levels (4mV) divided by the time window (1μs). Thus the slope is 4mV/μs.</li> | |||
<li> Setting the "When" option to raising and >, will trigger the scope only when it sees a signal that has a positive (raising) slope that is greater than the set level (4mV/μs). You could also set When option to trigger off slopes that are less than than the set level or equal to the set level. These can be of use when you are looking at signals with a variety of frequencies and you wish to trigger only off some of them.</li> | |||
<li> Make sure you are in the raising and > option. Since we are using large frequencies, we should always have a slope that is quite large (hundreds or thousands of mV/μs).</li> | |||
</ul> | |||
<li> Use the scope's math menu to create a fourier transform of the signal. Set the horizontal axis of channel 1 to 200ns/division and the horizontal axis of the fourier transform for 1.25MHz/division. </li> | |||
<li> Have the function generator sweep the frequency between 500kHz and 10Mhz over 10s (make sure the sweep's trigger is set to internal so that it loops the sweep constantly). What do you note about the spectrum? How does it change as it approaches higher frequencies?</li> | |||
<li> Adjust the vertical scale of the spectrum. <i>Carefully</i> estimate the frequency at which the height drops to around 1/2 its lower-frequency voltage (a change of -3dB). Liberal use of pausing the oscilloscope from recording data via the "Run/Stop" button might help this. It might also help you to change the range of the frequency sweep to "zoom in" on frequencies.</li> | |||
<li> Look up the data sheet for the BLP-5+. Does your estimate for the 3dB drop above agree with the data sheet? | |||
</ol> | |||
To look at filtering, we will use a mixer for frequency up-conversion. So, attach channel 2 (5MHz, 0.25V amplitude) to the LO port of the mixer, Channel 1 (4MHz, 0.25V amplitude) | |||
Latest revision as of 18:46, 11 January 2022
RF (short for Radio Frequency) signals are sinusoidal waves with frequencies in the MHz and GHz range.
While there are RF sources designed specifically for these frequencies, our good friend the Rigol Function Generator can produce frequencies in the lower end of the RF spectrum and should be sufficient for investigating RF signals. These were discussed in detail here. You should review their operation if needed, especially the section on performing Fourier Transforms, as they will be used extensively below.
For this module, you will need
- Rigol DG1022 Function Generator (or similar)
- Rigol DS1102E Oscilloscope (or similar)
- Micro-circuits ZAD-1 RF mixer
- A selection of BNC cables
- A few coaxial-to-BNC adaptors
- Thorlabs Variable Resistance Terminator
Measuring RF Power
Connect the output of channel 1 of the function generator through the terminator (set to 50ohm) to channel 1 of the oscilloscope.
- Set channel 1 of the function generator to create a 1V amplitude sine wave with a frequency of 4MHz.
- Set the horizontal and vertical scales of the scope to view the wave. Make sure the trigger for the scope is set to be on channel 1.
- Use the scope's measure function (or the scope's cursor) to get the amplitude of the wave. Is it what you expect? What is the amplitude if you remove the terminator? Does that make sense?
- Use the math menu to create a fourier transform of the signal. With the cursor, does the frequency the scope reads match what the setting from the scope? If it doesn't, why do you think that might be?
Termination and Impedance Matching
We discussed in the function generator and oscilloscope module the importance of impedance matching. To do this, we'll use a circulator (or, rather, a bi-directional coupler as a circulator). A circulator has three ports:, A, B and C. Signals that flow into port A is sent out of port B. Signals that flow into port B is sent out of port C. Signals that flow into port C are sent out of port A.
This is particularly useful for looking at impedance matching. As discussed in the function generator/oscilloscope module, if the impedances, measured in ohm, of two electrical elements signals that change in time can be reflected off one end and back towards the other end. If in between these two elements there is a circulator, the reflected signal will be sent to third port rather than going to the original source of the signal. Measuring the voltage on this third port lets us measure the signal that is reflected from one of the circuit elements.
- Attach the coupler as follows
- The output of Channel 1 of the signal generator should be attached to the OUTPUT port of the coupler. This is port A of the circulator.
- The INPUT port of the coupler should be attached directly to channel 1 of the oscilloscope. This is port B of the circulator.
- The COUPLED port of the coupler should be attached, through a 50-ohm terminator, to channel 2 of the oscilloscope. This is port C of the circulator.
- In this configuration, the signal from the function generator will flow through port A (output) to port B (input) and then to the oscilloscope's channel 1. Any of that signal that is reflected from channel 1 will flow into port B (input) to port C (coupled) and then to the oscilloscope channel 2.
- Yes, it's weird that port A of the circulator is the input port of the coupler, but functioning as a circulator is not really the purpose of the coupler, which is nominally used to combine two signals (from the input and the coupled ports) into an output port. But, it can function as a circulator (or sometimes called a "reflectometer") so we'll use it as one.
- Good job! Now disconnect what you just connected. We're going to use a different setup first.
- Connect the output of channel 1 of the function generator directly to channel 1 of the oscilloscope. Set the frequency of the function generator to create a 0.5V amplitude, 5Hz sine wave.
- Set the oscilloscope to trigger off channel 1 in edge mode and set the trigger level to something value a little larger than 0V (but less than 0.5V, of course). Make sure the vertical axis of the scope will show the entirety of your wave and the horizontal axis should be at least 100ms/division.
- In the trigger menu of the oscilloscope, change the sweep type to single - this will record a single (duh) trace of the oscilloscope when it is triggered and display just that one trace. The screen should erase any plot and the tun/stop button should turn green. If it red, press it and the screen should clear. The scope is now waiting for a trigger.
- On the function generator, press the "burst" button. Use the blue buttons under the scope the set the mode to "Ncycle" (the first menu option, don't set it to gated), the number of cycles should be 1, the phase should be 0 and the delay should be 0s. Now press the button under "Trigger" and then the button under "Source". Change the source to "Manual" and stay in this menu. Pressing the button under "manual" again will create a pulse as you defined it above. Try it.
- Did that work? Good. Trigger the function generator again. What happened with the oscilloscope? Pressing the red "RUN/STOP" button will clear the screen and allow you to trigger it again. Do this. Cool, huh?
- Now change the output of channel 1 to a 4MHz square wave. Change the horizontal scale of the oscilloscope so that it can show your wave (in burst mode, the frequency is really only setting the period of the wave as there isn't really a frequency as the wave won't repeat).
- NOW, attach the coupler as discussed above. Trigger the scope. Any signal on channel 2 is the signal that is reflected from the oscilloscope's channel 1 input. Weird, huh?
- Put the variable terminator in line with the input to channel 1 of the oscillosope. Repeat the triggering for various termination resistances.
- Note how the height of the reflected signal and the height of the measured signal change with the termination resistance, specifically how does the measured signal voltage compare to the output voltage when you terminate with 50-ohm?
- Why is a 50-ohm terminator often referred to as a 3dB?
- How does the phase of the reflected wave compare to that of the original wave? For this, you may want to have the terimator's resistance high and use a sine wave.
- How does this compare to reflections for light off a medium with a higher refractive index? How does it compare to reflections of light off a medium with a lower refractive index?
- Add another variable terminator to the input to channel 1 (it should have two connected together now). Set both terminators to 50ohm.
- What is the total input impedance of the oscilloscope now?
- How does this compare to the 50ohms impedance of the function generator?
- What happened to the phase of the reflected wave? How does it compare to the original wave?
- Does this agree with the your comparison to reflected light waves above? Complete the table below.
| Light (Refractive Index) |
Electrical Signal (Impedance) | |
|---|---|---|
| Reflection off lower index/impedance medium |
||
| Reflection off higher index/impedance medium |
Change in Phase after Reflection
Splitters
Splitters are fairly straight forward as they just split an RF signal into two outputs.
- Plug the output of channel 1 of the function generator into the S port of the splitter. Connect the two channels of the oscilloscope to outputs 1 and 2 of the splitter (make sure you match impedance appropriately).
- Set the output of channel 1 to 10Mhz and a 1V amplitude.
- What is the frequency of each wave on the oscilloscope? Does it agree with your 10MHz input? If it doesn't, why not?
- Estimate the amplitudes of the two waves on the oscilloscope. How doe they compare to the input amplitude from the function generator? Why do you think they are related this way?
- Estimate any phase difference between the two signals on the oscilloscope. How does that phase difference compare to the phase difference listed in the data sheet for the splitter?
You can also use splitters as combiner.
- Put a 3MHz, 1V amplitude sine wave into port 1 of the splitter.
- Put a 7MHz, 1V amplitude sine wave into port 2 of the splitter.
- Connect the S port of the splitter to the oscilloscope and and take a fourier transform of the signal. What frequencies are present?
Mixers
Mixers combine RF frequencies, either taking their sum or their difference. Each mixer has 3 inputs
- Local Oscillator(LO)
- Radio Frequency (RF)
- Intermediate Frequency (IF)
The LO port is always an input. The other two ports change whether they are an input or output depending on your application. For simplicity, we'll assume that the LO signal is always the largest of the two inputs.
If you would like an output that is SMALLER than 2nd (non-LO) input, the RF port is the input and the IF port is the output. Specifically, the output, IF, is the difference between the inputs:
This is called down-conversion, as it takes two signals and creates a third that is lower in frequency than both of them.
If, on the other hand, you want to create a signal that is larger than the inputs, the RF is the output and the IF is in the input:
additionally, you will actually get a 2nd frequency that is (again) the difference between the inputs:
This is called upconversion because it creates two signals that are larger than the input signal (unless, of course, the IF input is larger than half the LO signal).
The two conversion types are illustrated below.
This is how mixers work ideally, but in practice the output signals contain many combinations of the input signals, which can be confusing. We'll see that below. Additionally, because the frequencies are being combined, the waveforms that are produced is very complex and difficult to analyze just from looking at it, so we'll use the FFT function of the oscilloscope to look at the spectrum of the created wave.
We'll look at down-conversion first.
- Use channel 2 of the function generator as the LO input and set it t0 4MHz and an amplitude of 0.25V.
- Use channel 1 of the function generator as the RF input and set the amplitude to 0.25V. Set the frequency to 3MHz.
- Connect the IF output of the mixer to channel 1 of the oscilloscope. Set the horizontal scaling to 500ns/division.
- How does the signal look? Use the Y-cursor on the oscilloscope to estimate some frequencies you see in the signal (recall that the cursor menu automatically shows you frequency information as where is the difference between the locations of cursors A and B).
- Now have the function generator perform a fourier transform on the data. Adjust the scales of the math window appropriately. Use the cursors to estimate the frequencies of the peaks shown. Does this agree with what you measured above?
- Adjust the frequency of channel 1 and observe how the shape of the wave changes and how the locations of the peaks in the FFT change.
- Obviously, this mixer is not perfect. Rather than just getting the difference between the two signals, you get a bunch of other combinations of them of the form where n and m can be any integer (including negative values).
- For an ideal mixer, what are the values for n and m?
- For each peak in the spectrum, what values are the appropriate values for m and n? (hint, you might be helped by looking at how the peaks move if you change the RF frequency a little).
- What do you note about the values of m and n?
Now, let's look at up-conversion.
- Use channel 2 of the function generator as the LO input and set it t0 4MHz and an amplitude of 0.25V.
- Use channel 1 of the function generator as the IF input and set the amplitude to 0.25V. Set the frequency to 3MHz.
- Connect the RF output of the mixer to channel 1 of the oscilloscope. Set the horizontal scaling to 500ns/division.
- How does the spectrum of the signal compare to the down-conversion spectrum?
- What frequencies of the largest few peaks in the spectrum?
Using the mixer as you have above is effectively doing a heterodyne measurement on the signal. A heterodyne measurement takes two signals with different frequencies and measures the frequency difference and sum between them. This is a common technique in optics experiments (although often the sum of two frequencies for optical signals is well beyond the limits of a photo-detector).
There is a another technique called a homodyne measurement, which uses the same (hence, homodyne) signal for both the LO signal and the RF/IF signal after something has been done to the RF signal so we actually get a frequency difference. Let's see why this is useful.
- Use the mixer as a down converter and look at a 6MHz LO and 3MHz RF signal on channel 1 of the oscilloscope (including looking at the fourier transform
- Use a splitter to make a copy of a 3MHz, 1V amplitude signal from channel 1 of the function generator.
- Attach one
Attenuation and Filtering
Attach channel 1 of function generator through one of the 5MHz low-pass filters to the oscilloscope (note that the low-pass filter is 50-ohm terminated, so we don't need to use a terminator). The function generator should produce a 0.25V amplitude sine wave.
- Set the scope to trigger on channel 1, but set the trigger mode to "slope" - that is the scope will trigger based on what the slope of the signal is. Set the 'When" menu to the top option - a rising slope with a greater than symbol (>). This will trigger the scope whenever it encounters a slope that is larger than a set value.
- To set this value, use the "time" menu item to look at how the signal changes over some window. Set it to 1 μs, so that the voltage on channel 1 is compared over a range of 1us.
- Use the trigger level knob to change the "upper level" of the change you are looking for. The "low level" is set to -4mV. The difference between the two level is the voltage change you are looking for to trigger from. Set the Up Lvl to 0 mV.
- So, the trigger slope is the difference between the levels (4mV) divided by the time window (1μs). Thus the slope is 4mV/μs.
- Setting the "When" option to raising and >, will trigger the scope only when it sees a signal that has a positive (raising) slope that is greater than the set level (4mV/μs). You could also set When option to trigger off slopes that are less than than the set level or equal to the set level. These can be of use when you are looking at signals with a variety of frequencies and you wish to trigger only off some of them.
- Make sure you are in the raising and > option. Since we are using large frequencies, we should always have a slope that is quite large (hundreds or thousands of mV/μs).
- Use the scope's math menu to create a fourier transform of the signal. Set the horizontal axis of channel 1 to 200ns/division and the horizontal axis of the fourier transform for 1.25MHz/division.
- Have the function generator sweep the frequency between 500kHz and 10Mhz over 10s (make sure the sweep's trigger is set to internal so that it loops the sweep constantly). What do you note about the spectrum? How does it change as it approaches higher frequencies?
- Adjust the vertical scale of the spectrum. Carefully estimate the frequency at which the height drops to around 1/2 its lower-frequency voltage (a change of -3dB). Liberal use of pausing the oscilloscope from recording data via the "Run/Stop" button might help this. It might also help you to change the range of the frequency sweep to "zoom in" on frequencies.
- Look up the data sheet for the BLP-5+. Does your estimate for the 3dB drop above agree with the data sheet?
To look at filtering, we will use a mixer for frequency up-conversion. So, attach channel 2 (5MHz, 0.25V amplitude) to the LO port of the mixer, Channel 1 (4MHz, 0.25V amplitude)





